Question

Use calculus to find the absolute maximum and minimum values of the function. (round all answers to three decimal places.) f(x) = x + 2cos(x) [0, 2]olute minimum values of f on the given interval. f(x) = e-x - e-2x [0, 1]

Answer 1

Part A:

Given the function
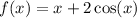
`f(x)=x+2\cos(x)`, the absolute maximum or minimum occurs when
`f'(x)=0`.


`f'(x)=0 \\ \\ \Rightarrow1-2sin(x)=0 \\ \\ \Rightarrow2sin(x)=1 \\ \\ \Rightarrowsin(x)= (1)/(2) \\ \\ \Rightarrow x=\sin^(-1){(1)/(2)}= (\pi)/(6)`

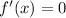
Using the second derivative test,


`f''(x)=-2cosx \\ \\ \Rightarrow f''\left( (\pi)/(6) \right)=-2\cos{\left( (\pi)/(6) \right)}=-1.732`

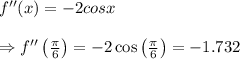
Since the second derivative gives a negative number, the given function has a maximum point at
`x=(\pi)/(6)`.

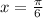
And the maximum point is given by:


`f\left( (\pi)/(6) \right)=(\pi)/(6)+2\cos\left( (\pi)/(6) \right) \\ \\ =0.5236+2(0.8660)=0.5236+1.732 \\ \\ =\bold{2.256}`

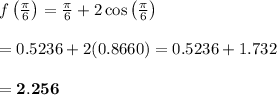
i.e.
`\left((\pi)/(6),\ 2.256\right)`



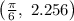
Part B:

Given the function
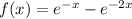
`f(x)=e^(-x)-e^(-2x)`, the absolute maximum or minimum occurs when
`f'(x)=0`.


`f'(x)=0 \\ \\ \Rightarrow-e^(-x)+2e^(-2x)=0 \\ \\ \Rightarrow2e^(-2x)=e^(-x) \\ \\ \Rightarrow2e^(-x)=1 \\ \\ \Rightarrow e^(-x)=(1)/(2) \\ \\ \Rightarrow-x=\ln (1)/(2)=-0.6931 \\ \\ \Rightarrow x=0.6931`

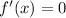
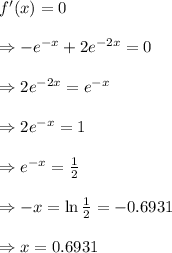
Using the second derivative test,


`f''(x)=e^(-x)-4e^(-2x) \\ \\ \Rightarrow f''(0.6931)=e^(-0.6931)-4e^(-2(0.6931)) \\ \\ =0.5-4e^(-1.386)=0.5-4(0.25)=0.5-1 \\ \\ =-0.5`

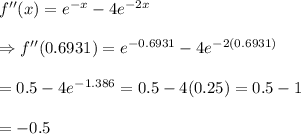
Since the second derivative gives a negative number, the given function has a maximum point at
`x=0.6931`.

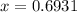
And the maximum point is given by:


`f(0.6931)=e^(-0.6931)-e^(-2(0.6931)) \\ \\ =0.5-e^(-1.386)=0.5-0.25=\bold{0.25}`

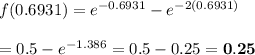
i.e. (0.693, 0.25)