Question

The grades on a math test are shown in the table. make a box plot for the data

Answer 1

A boxplot is a standardized way of displaying the distribution of data based on a five-number summary (“minimum”, first quartile (Q1), median, third quartile (Q3), and “maximum”). It can tell you about your outliers and what their values are.

To draw a boxplot, we need to get the five numbers outlined in the definition above from the data provided. The data provided has to be arranged in ascending order. This is shown below:

`63,75,76,78,80,81,87,89,91,91,95,100`

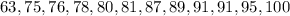
Minimum Number: 63

Maximum Number: 100

Median: The median position is calculated using the formula

`Q2=(n+1)/(2)`

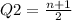
where n is the number of data in the set.

For the question provided, the number of terms is 12. Therefore, the median position is:

`Q2=(12+1)/(2)=(13)/(2)=6.5`

The 6.5th position is gotten by finding the average of the 6th and 7th terms. This is shown below:

`Q2=(81+87)/(2)=(168)/(2)=84`

First Quartile: The position of the first quartile is gotten using the formula:

`\begin{gathered} Q1=(1)/(4)(n+1) \\ \therefore \\ Q1=((12+1))/(4)=(13)/(4)=3.25 \end{gathered}`

The 3.25th position is gotten by multiplying the preceding term of the position by 0.25 and the following term by 0.75 and then finding the sum. This is done below:

`\begin{gathered} 3rd\Rightarrow76 \\ 4th\Rightarrow78 \\ \therefore \\ Q1=(76*0.25)+(78*0.75)=19+58.5=77.5 \end{gathered}`

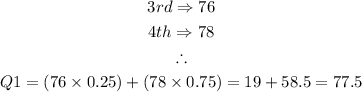
Third Quartile: The position of the third quartile is gotten using the formula:

`\begin{gathered} Q3=(3)/(4)(n+1) \\ \therefore \\ Q1=(3(12+1))/(4)=(3*13)/(4)=(39)/(4)=9.75 \end{gathered}`

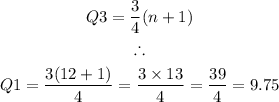
The 9.75th position is gotten by multiplying the preceding term of the position by 0.75 and the following term by 0.25 and then finding the sum. Since both the 9th and 10th terms are 91, then the value of Q3 is 91.

Boxplot

This is shown below: