Question

Prove that in a parallelogram each pair of consecutive angles are supplementary.

Answer 1

Given:

The objective is to prove that each pair of consecutive angles of a parallelogram are supplementary angles.

Step-by-step explanation:

Consider a parallelogram ABCD with opposite parallel sides.

First consider the parallel sides AB || CD. Then, the sides AD and BC are transversal lines.

By the property of parallel lines, the sum of the angles on same side of a transversal is 180°.

`\begin{gathered} \angle A+\angle D=180\degree\text{ . . . . (1)} \\ \angle B+\angle C=180\degree\text{ . . . . (2)} \end{gathered}`

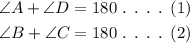
Now, consider the parallel sides as AD || BC. Then, the sides AB and CD are transversal lines.

By the property of parallel lines, the sum of the angles on same side of a transversal is 180°.

`\begin{gathered} \angle A+\angle B=180\degree\text{ . . . . . (3)} \\ \angle C+\angle D=180\degree\text{ . . . . . . .(4)} \end{gathered}`

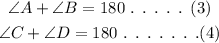
Thus, the sum of any two sides of a parallelogram will always be 180°.

Hence, it is proved that in a parallelogram each pair of consecutive angles are supplementary.