(-2, 4)
Step-by-step explanation:
The given equations:
3x - 2y = - 14 ...(1)
5x + 10y = 30 ...(2)
Using substitution method:
From equation 1:
3x - 2y = -14
3x = 2y - 14
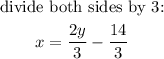
substitute for y in equation 2:
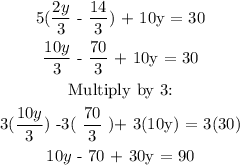
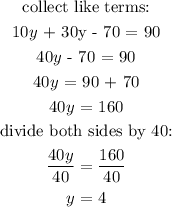
substitute for y in equation 1:
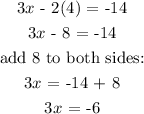
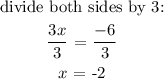
The solution in ordered pair (x, y) is (-2, 4)