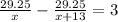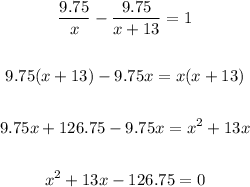Given:
Wyatt jogged to his friend's house 29.25 miles away and then got a ride back home.
It took him 3 hours longer to jog there than ride back.
His jogging rate was 13 mph slower than the rate when he was riding.
Required:
To find the jogging rate.
Step-by-step explanation:
Assume his jogging rate is x mph.