Question

The answer I got (4 +/- sqrt -68 over 6) is literally none of the answers. What did I do wrong??

Answer 1

D.
`x=(2+/- i√(17)))/(3)`

Explanation:

The quadratic formula is
`(-b+/- √(b^2-4ac))/(2a)`

a=-3

b=4

c=-7

Plug the variables in.

You get
`x=(-4+/- √(4^2-4(-3)(-7)))/(2(-3))`

Simplify.

`x=(2+/- i√(17))/(3)`

You might have just put solved incorrectly or put the numbers in the wrong spots.

Answer 2

`x= (2 \pm i√(17))/(3)`

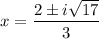
Explanation:

A complex number is the sum of a real number and an imaginary number.

An imaginary number is a non-zero real number multiplied by the imaginary unit
`i`.

`i=√(-1) \implies i^2=-1`

For example:

• 5
  `i` is an imaginary number (and its square is -25)
• 5 + 5
  `i` is a complex number

Quadratic Formula

`x=(-b \pm √(b^2-4ac) )/(2a)\quad\textsf{when }\:ax^2+bx+c=0`

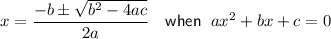
Given quadratic equation:

`-3x^2+4x-7=0`

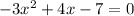
Therefore:

`a=-3, \quad b=4, \quad c=-7`

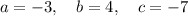
Inputting these values into the quadratic formula:

`\begin{aligned}\implies x & =(-4 \pm √(4^2-4(-3)(-7)))/(2(-3))\\\\ & = (-4 \pm √(-68))/(-6)\\\\ & = (-4 \pm √(4 \cdot -17))/(-6)\\\\ & = (-4 \pm √(4)√(-17))/(-6)\\\\ & = (-4 \pm 2√(-17))/(-6)\\\\ & = (2 \pm √(-17))/(3)\\\\ & = (2 \pm √(-1 \cdot 17))/(3)\\\\ & = (2 \pm √(-1)√(17))/(3)\\\\ & = (2 \pm i√(17))/(3)\end{aligned}`

Therefore, the solutions to the given quadratic equation are complex numbers as they include the imaginary number
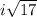`i√(17)`.