Question

A tank in the shape of an inverted right circular cone has height 1010 meters and radius 1111 meters. it is filled with 66 meters of hot chocolate. find the work required to empty the tank by pumping the hot chocolate over the top of the tank. note: the density of hot chocolate is δ=1530kg/m3δ=1530kg/m3

Answer 1

I'm going to use integral calculus

first draw a diagram (do it youerslef)

if we imagine a small slice going horizontally through the cone, we can find the work for that slice and integrate from the bottom to top

first assign a coordinate plane
the origin is at the pointy part (bottom) of cone

ok
so Δwork=force times distance

force=mass times acceleration
acceleration=g=9.8m/s^2
mass=density times volume
mass=1350kg/m^3 times pir^2 times the thickness (Δy because in y direction)
r=x

distance=distance the piece must be raised=height-y=10-y


so we got
Δwork=(1350kg/m^3)(π)(x²)(10-y)gΔy
we need to find an equation to write x in terms of y
see our coordinate plane

ok, so if we say one side is a line on the graph, we see a line passing through the origin with rise 10m and run 11m, so slope is 10/11
y=(10/11)x is the equation
so now solve for x
y(11/10)=x
subsitute
Δwork=(1350kg/m^3)(π)((y(11/10)²)(10-y)gΔy
now integrate from y=0 to y=10

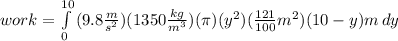
`work= \int\limits^(10)_0 {(9.8(m)/(s^2))(1350(kg)/(m^3))(\pi)(y^2)((121)/(100)m^2)(10-y)m} \, dy` m is meters and s is seconds and kg is kilograms
my calculator's broken so do the integration yourself
here's a simpified form:

`work= (9.8(m)/(s^2))(1350(kg)/(m^3))(\pi)((121)/(100)m^2)\int\limits^(10)_0 {(y^2)(10-y)m} \, dy`