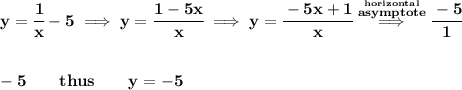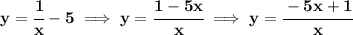
to find the vertical asymptotes, is simply check what makes the denominator to 0 whilst not zeroing out the numerator, clearly is just x = 0, thus that is the vertical asymptote.
now, for the horizontal asymptote, notice, the degree of the numerator is the same degree of the denominator, thus the horizontal asymptote is at at the fraction whose value is from the coefficients of the leading terms,