Question

We can find s , the slant height using Pythagorean theorem , and since this solid is made of parts of simple solids , we can combine the formulas to find surface area and volume

Answer 1

EXPLANATION

Given that the slant represents the diagonal side of a solid, we can use the Pythagorean Theorem as shown as follows:

Thus, if we know the height and the base, we can compute the slant height by the Pythagorean as explained above.

The Pythagorean Theorem says:

Therefore, we can substitute the radius and the height in the Pytagorean Equation to obtain the slant height.

`\text{radius}^2+\text{height}^2=\text{slant height\textasciicircum{}2}`
`r^2+h^2=s^2`

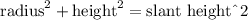
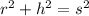
Pluggin in the given values into the equation:

`5^2+7^2=s^2`

Isolating the slant height:

`\sqrt[]{5^2+7^2}=s`

Now, if we need to compute the Surface Area, we need to combine the formulas for all the solids that form the figure.

Figure:

Thus, the surface area is:

`Total\text{ Surface Area=}\frac{SurfaceArea_{\text{sphere}}}{2}+Surface\text{ Area of the Cone}-\text{ Surface Area of the Base}`

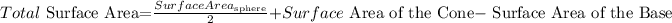
Replacing terms:

`=(4\cdot\pi\cdot r^2)/(2)+(\pi rs+\pi r^2)-\pi r^2`

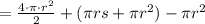
We can apply the same reasoning to the Volume:

`Total\text{ Volume}=\frac{Volume\text{ Sphere}}{2}+Volume\text{ of the cone}`
`=((4)/(3)\pi r^3)/(2)+(1)/(3)\pi r^2h`

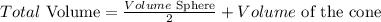
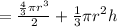
Finally, just replacing the corresponding values, give us the appropiate surfaces and volumes.