Question

Properties of chords. leave answer in simplest form. DONT TAKE FOREVER TO ANSWER

Answer 1

Let's put more details in the figure to better understand the problem:

To be able to determine DC, let's treat this as two similar triangles and apply ratio and proportion.

We get,

`\text{ }\frac{\text{ AB}}{\text{ OB}}\text{ = }\frac{\text{ EF}}{\text{ OE}}`
`(18)/(12)\text{ = }\frac{x}{\text{ 10}}`
`\frac{18\text{ x 10}}{12}\text{ = }x`
`(180)/(12)\text{ = }x`
`15\text{ = }x`
`\text{ FE = 15}`

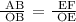
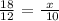
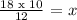
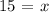
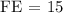
If a diameter or radius is perpendicular to a chord, then it bisects the chord and its arc. Therefore, we can say that FE = ED.

Determining the length of FD, we get:

`\text{ FE + ED = FD}`
`\text{ FE + FE = FD}`
`\text{ 15 + 15 = FD}`
`\text{ FD = 30}`

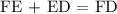
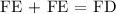
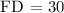
Therefore, FD = 30