Question

1.Given a∥b , and c is not parallel to a or b, which statements must be true?

Select each correct answer.

m∠7=m∠11

m∠5=m∠12

m∠4=m∠5

m∠1=m∠5

2.In the figure, AB¯¯¯¯¯∥CD¯¯¯¯¯ and m∠4=85°.

What is m∠5?





Enter your answer in the box.

Answer 1

1. is m∠4=m∠5 by the alternate interior angle theorem.
2. Angles 4 & 3 are supplementary angles or linear pair and so they have to equal 180 and 180 - 85= 95 3 & 5 are corresponding angles so 95 should be your answer.

Answer 2

1. We have been given that a∥b , and c is neither parallel to a nor b.

Let us see which of our given options are correct.

A. m∠7 can not be equal to m∠11 as line c is not parallel to line a.

B. m∠5 can not be equal to m∠12 as line c is not parallel to line b.

C. By alternate interior angles m∠4=m∠5 as ∠4 is inside line a and ∠5 is inside line b. Both angles are on the opposite sides of transversal.

D. Since we know that corresponding angles are congruent. We can see that ∠5 corresponds to ∠1, therefore, m∠1=m∠5.

Therefore, Option C and D are correct choices.

2. We have been given that AB∥CD and m∠4=85°. We are asked to find measure of ∠5.

Since we know that same side interior angles are supplementary. In our figure we can see that ∠4 and ∠5 are same side interior angles.

`\measuredangle 4+\measuredangle 5=180^(o)`

`85^(o)+\measuredangle 5=180^(o)`

`\measuredangle 5=180^(o)-85^(o)`

`\measuredangle 5=95^(o)`

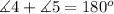
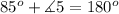
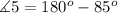
Therefore, measure of ∠5 will be 95 degrees.