Question

Two forces are acting on an object at the same point. Determine the angle between the two forces.

F1 = 〈-1,4〉
F2 = 〈3,-1〉

54°
122°
234°
304°

Answer 1

I think the answer is 122, key is to make a body diagram with the origin as the same point. see the forces are opposing ? F1 is in 2nd quadrant, F2 is in 3rd quadrant. Inverse tangent gives the angle between the force and x-axis.

the angle between is:
180 - arctan(4) + arctan(1/3) = 122

Answer 2

122°

Explanation:

To find the angle between two vectors (forces are vectors), we need to use

`cos\theta=(F_(1) * F_(2) )/(|F_(1)| * |F_(2)|)`

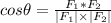
Where

`F_(1)=-1i+4j`

`F_(2)=3i-1j`

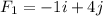
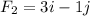
First, we need to find the length of each vector

`|F_(1)|=\sqrt{(4)^(2)+(-1)^(2) } =√(16+1) =√(17) \\|F_(2)|=\sqrt{(-1)^(2)+(3)^(2) } =√(1+9) =√(10)`

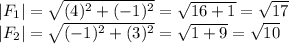
Then, we calculate the fot product of the vectors

`F_(1) * F_(2)=(-1)(3)+(4)(-1)=-3-4=-7`

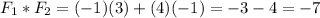
Now, we replace all in the formula

`cos\theta=(-7)/(√(17) * √(10) ) =-(7)/(√(170) ) \\\theta = cos^(-1)(-(7)/(√(170) )) \approx 122.6 \°`

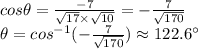
Therefore, the right answer is the second choice 122°.