Greetings!
Let l represent the
length of the rectangle.
Let w represent the
width of the rectangle.
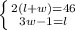 Isolate
Isolate for the l in Equation #2.
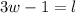
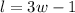 Substitu
Substitute
Equation #2 into Equation #1.
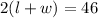
![2[(3w-1)+w)]=46](https://img.qammunity.org/2018/formulas/mathematics/high-school/wymom8ear9pw3pzfo6rmdzfeubutsj9x1t.png) Combine
Combine Like Terms.
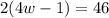 Distribute
Distribute the Parenthesis.
How?
Multiply the terms inside the Parenthesis by the term outside of the Parenthesis.
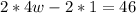
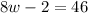
Add 2 to both sides.
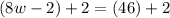
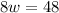
Divide both sides by 8.
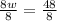
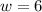
The Answer Is:
![\left[\begin{array}{ccc}w=6\end{array}\right]](https://img.qammunity.org/2018/formulas/mathematics/high-school/tpu8xkjtpd9em69416tw5l2dx9g9dgkl0e.png)
The Width is 6 units and the Length is 17 units.
Hope this helps.
-Benjamin