Question

Given the equation Square root of 8x plus 1 = 5, solve for x and identify if it is an extraneous solution.

Answer 1

do recall that squaring and the *radical sign* cancel each other out... like so:(
`√(a)`)
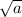
`^(2)`= a

When you put it that way, it isn't enough :P
(
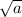
`√(a)`)
`^(2)`= a
(
`√(8x+1)`)
`^(2)`=?

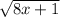
so you start with
(
`√(8x+1)`)
`^(2)`=
`(5)^(2)`
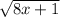
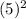
8x+1=25 <-- subtract 1 to both sides
8x=24 <- divide 8 to both sides
x= 3

To find out if it's an extraneous solution ask yourself: It mustn't result in a radical that I like to call... 'illegal'. Plug it into the radicand 8x+1 and make sure you get something that is not a negative number.... so, DO you get a negative number when you plug in x = 3 into the radicand?

(extraneous solution is a invalid solution)

x=3 not extraneous

Answer 2

Answer with explanation:

The given equation is

`√(8 x +1)=5\\\\ \text{Squaring both sides}}\\\\ 8x +1=25\\\\ 8 x=25-1\\\\8 x=24\\\\x=(24)/(8)\\\\x=3`

Substituting the value of , x=3, in original equation

LHS

`\rightarrow√(8* 3 +1)\\\\√(25)=5`

=R HS,

So, x=3, is not an extraneous solution.