Question

Last edit was seconds ago Format Slide Arrange Tools Add-ons Help Accessibility Background Layout- Theme Transition {(-1,5),(-2,2), (-3,0)} CARD SORT {(-2,0).(-4,2), (-6,0)} Linear Non-Linear {(-1,4), (-2,2), (-3,0)} {(-2,-1),(0, -2).(-2,-3)} {(2,1),(4,3), (6,5)} {(2,3), (2,2),(1,1)) CARD SORT: ORDERED PAIRS

Answer 1

Answer: We have to find if the ordered pairs are linear or non-linear.

`(-1,5)\text{ (-2,2) (-3,0)}`

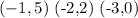
Linear equations are of the form:

`y(x)=mx+b`

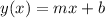
where:

`\begin{gathered} m=(\Delta y)/(\Delta x) \\ b=y-\text{intercept} \end{gathered}`

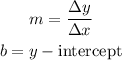
If we plot these three coordinate points, we get the following.

According to this graph, the points do seem to be on the same line:

Confirmation through the equation of the line:

`\begin{gathered} y(x)=mx+b \\ \therefore\rightarrow \\ m=(\Delta y)/(\Delta x)=(2-0)/(-2--3)=2 \\ \\ \rightarrow \\ 0=2(-3)+b\rightarrow b=6 \\ \therefore\rightarrow \\ y(x)=2x+6 \end{gathered}`

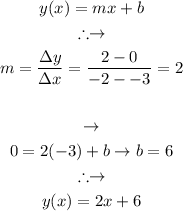
Plotting the equation on the same graph:

Therefore, we can conclude that these three points are not-linear because only two points lie on the same line.

Confirmation through algebraic approach would be as follows:

• Find slope and y-intercept from any two points

• And, confirm the resultant equation with the three coordinate points

The above steps will ensure the answer.