Question

A movie with an aspect ratio of 1.85:1 is shown as a letterboxed image on a 72 with a 16:9 inch television. Calculate the area of the TV and the area of the image ( round to the nearest whole number)

Answer 1

Given;

The movie aspect ratio is;

`1.85\colon1`

Size of the diagonal of the Televison;

`72\text{ inches}`

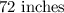
Ratio of the sides of the Television;

`16\colon9`

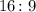
Using the ratio and a factor x we can find the width and height of the television.

The width will be;

`16x`

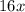
And height wil be;

`9x`

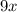
Using pythagoras theorem, since we have the value of the diagonal length of the Television;

`\begin{gathered} a^2+b^2=c^2 \\ (16x)^2+(9x)^2=72^2 \end{gathered}`

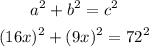
solving for x we have;

`\begin{gathered} 256x^2+81x^2=5184 \\ 337x^2=5184 \\ x^2=(5184)/(337) \\ x=\sqrt[]{(5184)/(337)} \\ x=3.922 \end{gathered}`

Since we have x, we can now substitute to get the width and height.

`\begin{gathered} \text{width w}=16x=16(3.922)=62.75\text{ inches} \\ \text{height h}=9x=9(3.922)=35.30\text{ inches} \end{gathered}`

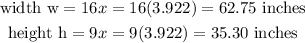
Now we can calculate the area of the Television from its width and height ;

`\begin{gathered} \text{Area A = Height }* Width \\ A=35.30*62.75 \\ A=2,215.075inch^2 \\ A=2,215inch^2 \end{gathered}`

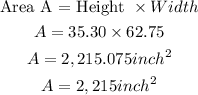
The area of the Television is 2,215 square inch

Next we need to find the Area of the image;

The height of the image is;

`\begin{gathered} \text{Height of image=}\frac{width\text{ of TV}}{\text{Aspect ratio}} \\ I_h=(62.75)/(1.85) \\ I_h=33.92 \end{gathered}`

The width of the image will be the same as the width of the TV since the Calculated height of image is less than the height