The average rate of change of a function in the interval [a,b] is given by:
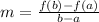
In this case we know that the interval is [-1,3] which means that a=-1 and b=3. This also means that we need to find f(-3) and f(-1); from the table we have:
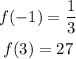
Once we know all the values, we need we plug them in the expression for the average rate of change:
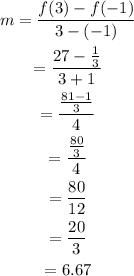
Therefore, the average rate of change of the function in that interval is 6.67.