Question

What are the classifications of each system? Drag the answer into the box to match each system. {4x−2y=102x−y=5 {y=2x−3−2x+y=−5 {2x−5y=143x+4y=10

Answer 1

the first one is. coincident
second. inconsistent
third. consistent independent

I just did this quiz (:

Answer 2

we know that

If a system has exactly one solution, it is a consistent independent system.

If a system has an infinite number of solutions, it is a consistent dependent system .

If a system has no solution, it is said to be inconsistent

We're going to solve each system to determine its classification

case A)

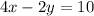`4x-2y=10` ------> equation A

`2x-y=5` ------> equation B

Multiply equation B by
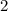`2` both sides

`2*(2x-y)=2*5` ----->
`4x-2y=10`

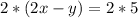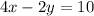
Equation A and equation B are the same line

Therefore

The system has an infinite number of solutions

The answer case A) is

The system is a consistent dependent system (coincident)

case B)

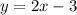`y=2x-3` ------> equation A

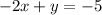`-2x+y=-5` ------> equation B

Isolate the variable y in the equation B

`y=2x-5`

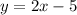
Both lines are parallel lines, because has the same slope

Therefore

The system has no solution

the answer case B) is

The system is inconsistent

case C)

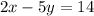`2x-5y=14` ------> equation A

`3x+4y=10` ------> equation B

Multiply equation A by
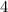`4` and equation B by
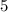`5` both sides

`4*(2x-5y)=4*14` ----->
`8x-20y=56`

`5*(3x+4y)=5*10` ----->
`15x+20y=50`

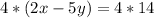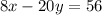
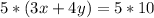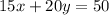
Adds the equations

`8x-20y=56 \\15x+20y=50\\-------\\8x+15x=56+50 \\23x=106 \\x=4.61`

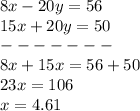
Find the value of y

`2*4.6-5y=14`

`y=-0.96`

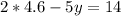
therefore

The system has one solution

The answer case C) is

The system is a consistent independent system