Question

A. Use the discriminant to determine the number and type of solutions for the quadratic equation.B. Graph the equation to verify the result that the discriminant indicated.C. Solve the equation by graphing, factoring, and the quadratic formula.D. What do you notice about each method?E. Describe what the solutions mean in context of the problem.

Answer 1

Given:

A ball is thrown upwards with a velocity of 7 m/s, It is thrown from a height of 11 meters above the ground.

`h=-4t^2+7t+11`

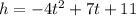
To find:

A) To determine the number and type of solutions using discriminant.

B) To draw the graph and verify the result of discriminant.

C) To solve the equation using graphing, factoring and quadratic formula.

D) Changes observed in each method.

E) To explain the answer in context of question.

Step-by-step solution:

A) we will determine the nature of roots using the discriminant:

`\begin{gathered} D=b^2-4ac \\ \\ D=(7)^2-4(-4)(11) \\ \\ D=49+176 \\ \\ D=225 \end{gathered}`

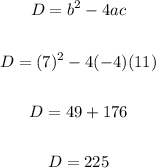
As D > 0, thus the roots of the equation will be real and unequal.

B)

We will now draw the graph to verify the result of the discriminant:

The graph of the equation states that there are 2 real roots of the equation which are unequal in nature.

C)

Using graphing:

From the graph there are 2 solutions:

A = 2.75

B = -1

Using factoring:

`\begin{gathered} 4t^2-7t-11=0 \\ \\ 4t^2-7t+((7)/(4))^2-((7)/(4))^2-11=0 \\ \\ (2t-(7)/(4))^2-((15)/(4))^2=0 \\ \\ (2t+2)(2t-(11)/(2))=0 \\ \\ t=-1,2.75 \end{gathered}`

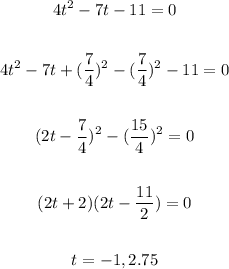
Using quadratic formula:

`\begin{gathered} t=(-b\pm√(b^2-4ac))/(2a) \\ \\ t=(-7\pm√((7)^2-4(-4)(11)))/(2(-4)) \\ \\ t=(-7\pm15)/(-8) \\ \\ t=-1,2.75 \end{gathered}`

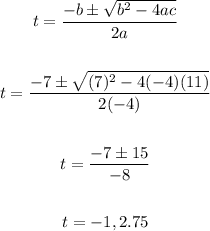
D)

From each method, we received the same answers but the quadratic formula is the most easy to use and formula-based approach.

E)

The solution describes that the ball is thrown upwards at t = 0 from h = 11, it reaches the ground at t = 2.75.