Question

Is y-7x=314x-2y=28 parallel, perpendicular, or neither

Answer 1

We are given the following two equations.

`y-7x=3\qquad and\qquad 14x-2y=28`

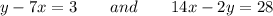
We are asked to find out whether these equations of lines are parallel, perpendicular, or neither​.

First of all, let us re-write these equations into the standard slope-intercept form.

This simply means to separate the y variable.

`\begin{gathered} y-7x=3 \\ y=7x+3\qquad eq.1 \end{gathered}`

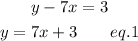
Similarly, for the other equation

`\begin{gathered} 14x-2y=28 \\ 14x=2y+28 \\ 14x-28=2y \\ 2y=14x-28 \\ y=(14x)/(2)-(28)/(2) \\ y=7x-14\qquad eq.2 \end{gathered}`

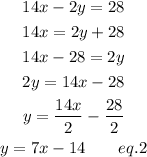
Now recall that the standard slope-intercept form is given by

`y=mx+b`

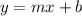
Where m is the slope and b is the y-intercept.

Comparing the standard form with our two equations we see that

Slope of 1st equation = 7

Slope of 2nd equation = 7

So the two equations have an equal slope.

Whenever two equations have equal slopes then the lines are parallel.

Therefore, the given equations are parallel.