Question

Triangle PQR is rotated, translated, and dilated to obtain triangle P'Q'R' as shown.

Answer 1

Two triangles are similar if they have the same ratio of corresponding sides and equal pairs of corresponding angles.

For the triangle and its image provided in the question to be similar, the angle measures must be equal and the corresponding side ratios must be equal as well, such that:

`(P^(\prime)Q^(\prime))/(PQ)=(P^(\prime)R^(\prime))/(PR)=(Q^(\prime)R^(\prime))/(QR)=scale\text{ }factor`

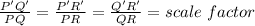
Assuming the angles are unchanged by the transformation, we can consider the side lengths:

`\begin{gathered} PR=3 \\ P^(\prime)R^(\prime)=4.5 \end{gathered}`

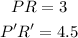
Therefore, the scale factor will be:

`scale\text{ }factor=(4.5)/(3)=(3)/(2)`

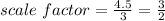
Hence, the two figures are similar because the angle measures are equal and each side length of the image is 3/2 times the corresponding side length of the preimage.

OPTION C is the correct option.