Question

Cody wants to attend the fall festival at school. The price of admission to the festival is $5.50 and each game costs an additional 75 cents. If Cody has $15.00 to spend at the festival, which inequality can be used to solve for g, the number of games that he can play, and what is the maximum number of games he can play?a) 5.50 +0.75g ≤ 15.00; 12 gamesb) 5.50 +0.75g ≤ 15.00; 13 gamesc) 0.75 +5.5g ≤ 15.00; 2 gamesd) 0.75 +5.5g ≤ 15.00; 3 games

Answer 1

Given:

a.) The price of admission to the festival is $5.50 and each game costs an additional 75 cents.

b.) Cody has $15.00 to spend at the festival.

The formula on the maximum number of games he can play is:

`\text{ Maximum no. of games can be played = Admission fee + Costs per game}`

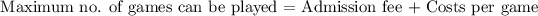
Letting g = the number of games that he can play, we get:

`\text{ 5.50 + 0.75g}`

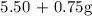
Since Cody has $15.00 to spend at the festival, the limit of the number of games he can play will be:

`\text{ 5.50 + 0.75g }\leq\text{ 15}`

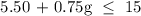
Let's now determine the maximum no. of games he can play,

5.50 + 0.75g ≤ 15

0.75g ≤ 15 - 5.50

0.75g ≤ 9.5

0.75g/0.75 ≤ 9.5/0.75

g ≤ 12.67

g ≤ 12

The maximum number of games that he can play is 12, he still has some money left but not enough to pay for the game cost.

Therefore, the answer is CHOICE A: 5.50 + 0.75g ≤ 15 ; 12 games