Question

Need help on number six. Need to use one of the kinematics equations

Answer 1

Since Stephanie serves the volleybal straight up this means that we have an uniform accelerated motion with acceleration equal to g, the acceleration of gravity. Assuming that upwards is the positive direction the acceleration g will be negative.

The equations we can use for an uniform accelerated motion are:

`v_f=v_0+gt`
`y-y_0=v_0t+(1)/(2)gt^2`
`v^2_f-v^2_0=2g(y-y_0)`

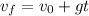
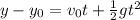
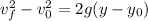
a.

The velocity of the ball when it reachs its original height will have the same magnitude as the initial veloctity but different direction. Let's prove this using the third equation. In this case the initial velocity is 7.6 m/s, the initial and final height are 0.8 meters and the gravity has a magnitude of 9.8 m/s^2. Plugging this values and solving for the final velocity we have:

`\begin{gathered} v^2_f-7.6^2=2(-9.8)(0.8-0.8) \\ v^2_f-7.6^2=0 \\ v^2_f=7.6^2 \\ v_f=\pm\sqrt[]{7.6^2} \\ v_f=\pm7.6 \end{gathered}`

Now, since the ball is falling in this instant we have to choose the negative sign; therefore the velocity when it reaches the original height is -7.6 m/s. (Notice how the magnitude is the same as the initial velocity like we stated above)

b.

To determine how long it takes to get to its maximum height we can use the first equation. We know that at this point the velocity has to be zero; otherwise the object would still be going up or it would be fallin already. Then we have that:

`\begin{gathered} 0=7.6-9.8t \\ 9.8t=7.6 \\ t=(7.6)/(9.8) \\ t=0.776 \end{gathered}`

Therefore it would take 0.776 seconds (rounded to three decimals) for the ball to reach its maximum height.