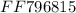We will investigate how to evaluate a function given an input value.
A function is defined as a unique relationship between an input and an output variable. Furthermore, for each value of an input there is a unique value of an output. In graphical terms all functions qualify the vertical line test.
A function is expressed in terms of an independent variable also called as an input variable. It is defined over the domain of indepedent variable which expresses a set of values that are of control, whereas, the output of a function depends on its domain.
We are given the following function as follows:
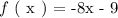
The above function is defined for all real values of ( x ) unless specified in the context of the problem. We can go ahead and write down the domain of the above function as follows:
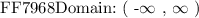
We are to evaluate the given function [ f ( x ) ] for one of the values from the domain expressed above i.e:
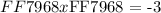
The operation of evaluating a function can be summarized as a substitution of the input value in the function's relationship and simplifying the result as follows:
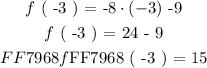
The above result of the function evaluation is as follows: