Question

Find the two x-values that are solutions to the absolute value equationbelow. *[5 - 2x] – 11 = 0

Answer 1

Given the definition of absolute value:

`\begin{gathered} |a|=\begin{cases}a,a\ge0 \\ -a,a<0\end{cases} \\ \end{gathered}`

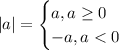
in this case we have the following:

`|5-2x|-11=0`

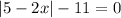
we will have two cases from this equation.

The first case is when 5-2x>=0, then we have the following:

`\begin{gathered} 5-2x-11=0 \\ \Rightarrow-2x-6=0 \\ \Rightarrow-2x=6 \\ \Rightarrow x=(6)/(-2)=-3 \\ x=-3 \end{gathered}`

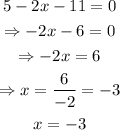
next, we will consider the cas when 5-2x < 0, then we would have the following:

`\begin{gathered} -(5-2x)-11=0 \\ \Rightarrow-5+2x-11=0 \\ \Rightarrow2x-16=0 \\ \Rightarrow2x=16 \\ \Rightarrow x=(16)/(2)=8 \\ x=8 \end{gathered}`

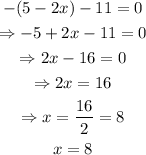
therefore, the two x-values that are solutions to the equation are x=-3 and x=8