Given the equation:
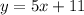
Let's find a set of parametric equation for the given equation given the parameter:
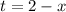
From the parameter:
t = 2 - x
Rewrite the parameter for x.
Rearrange the parameter:
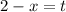
Subtract 2 from both sides:
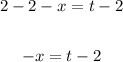
Divide all terms by -1:
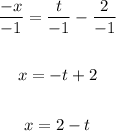
Now, substitute (2 - t) for x in the given equation:
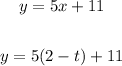
Simplify the equation using distributive property:
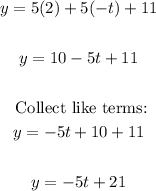
Therefore, the set of parametric equations is:
• x = 2 - t
,
• y = -5t + 21
ANSWER:
• x = 2 - t
,
• y = -5t + 21