We have the following equation system:
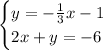
Those are two lines, to plot them you just need two points. The intercepts are the easiest points to calculate. Let's calculate for the first line:
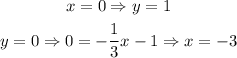
Then, this set of points belong to the first line:
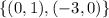
By the same logic, this set of points belong to the second line:
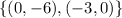
Ploting your system, it should look like this
Coincidentally, we already know the solution because it is on the x-intercept(the point (-3,0)). But let's calculate using our equations.
First, let's rewrite the second equation in slope intercept form.
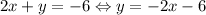
Now we match our equations:
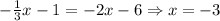
If you evaluate any of the functions at x = -