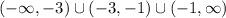Question

Hello! I was wondering what is the domain of this problem and the restriction of the domain and an explanation?

Answer 1

- The domain is simply all the possible x-values for which the rational function is defined.

- In order for us to find the domain, we simply need to find the vertical asymptotes of the function and then exclude them from the domain.

- The vertical asymptotes of a rational function is simply all the values of x, or in this case, t, that make the function undefined.

- Thus, we should equate the denominator to zero and then find the values of t. These values of t will be the values to exclude from the domain.

- Thus, we have:

`\begin{gathered} t^2+4t+3=0 \\ \text{ We can rewrite 4t as:} \\ 4t=3t+t \\ \\ t^2+3t+t+3=0 \\ \text{ Let us factorize} \\ t(t+3)+1(t+3)=0 \\ \\ (t+3)\text{ is common so we can factorize again,} \\ \\ (t+1)(t+3)=0 \\ \\ \text{ Thus, we have that:} \\ t+1=0\text{ or }t+3=0 \\ \text{ Subtract 1 and 3 from their respective equations} \\ \\ t=-1\text{ or }t=-3 \end{gathered}`

- Thus, the values to exclude from the domain are t = -1 and t = -3.

- Thus, the domain of the function is

`(-\infty,-3)\cup(-3,-1)\cup(-1,\infty)`