Question

An initial investment amount P, an annual interest rate r, and a time t are given. Find the future value of the investment when inte monthly, (c) daily, and (d) continuously. Then find (e) the doubling time T for the given interest rate. P = $2500, r = 3.95%, t = 8 yr a) The future value of the investment when interest is compounded annually is $ 3408.29 (Type an integer or a decimal. Round to the nearest cent as needed.) b) The future value of the investment when interest is compounded monthly is $3,427.30 - (Type an integer or a decimal. Round to the nearest cent as needed.) c) The future value of the investment when interest is compounded daily is $ 3429.02 Type an integer or a decimal. Round to the nearest cent as needed.) d) The future value of the investment when interest is compounded continuously is $ (Type an integer or a decimal. Round to the nearest cent as needed)

Answer 1

In the case of continuous compounding, the relevant formula is

`P(t)=P_0e^(rt)`

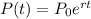
which can be derived from the usual compound interest formula in the limit n → ∞.

Puttting in P_0 = $2500, t = 8yr r = 3.95 gives

`P(8)=2500e^((0.0395*8))`
`\textcolor{#FF7968}{P(8)=3429.08}`

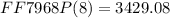
Hence, The future value of the investment when interest is compounded continuously is $3429.08