1 Answer

Ask a Question

Wouter Van Nifterick · Answer 1 · 2023-08-20T11:05:22+0000

SOLUTION

Step 1 :

In this question, we can carefully discover from the graph that:

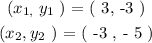
$\begin{gathered} (x_{1,\text{ }}y_{1\text{ }})\text{ = ( 3, -3 )} \\ (x_2,y_2\text{ ) = ( -3 , - 5 )} \end{gathered}$

Step 2:

We need to solve the gradient of the two points, using the formulae:

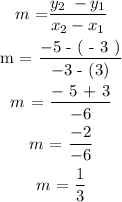
$\begin{gathered} m\text{ =}\frac{y_{2\text{ }}-y_1}{x_2-x_1} \\ \text{m = }\frac{-5\text{ - ( - 3 )}}{-3\text{ - (3)}} \\ m\text{ = }\frac{-\text{ 5 + 3}}{-6} \\ m\text{ = }(-2)/(-6) \\ m\text{ = }(1)/(3) \end{gathered}$

Step 3 :

Since the gradient, m =

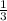
and the intercept on the y - axis to be c = -4

We can now use the equation of the line, y = m x + c,

$\begin{gathered} y\text{ = }(1)/(3)\text{ x - 4} \\ \text{Multiply both sides by 3, we have that :} \\ 3\text{ y = x - 12} \\ \operatorname{Re}-\text{arranging the equations, we have that:} \\ x\text{ - 3y - 12 = 0} \end{gathered}$

CONCLUSION: The equation of the line is x - 3y - 12 = 0.

0 Comments

Your comment on this question:

Your answer

1 Answer

0 Comments

Your comment on this answer:

Other Questions