Question

Which of the following equations represents the perpendicular bisector of WX graphed below?

Thank you! :)

Answer 1

The coordinates of the 2 given points are W(-5, 2), and X(5, -4).

First, we find the midpoint M using the midpoint formula:


`\displaystyle{ M_(WX)= ((x_1+x_2)/(2), (y_1+y_2)/(2) )= ((-5+5)/(2), (2+(-4))/(2) )=(0, -1).`

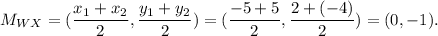
Nex, we find the slope of the line containing M, perpendicular to WX. We know that if m and n are the slopes of 2 parallel lines, then mn=-1.

The slope of WX is
`\displaystyle{ m= (y_2-y_1)/(x_2-x_1)= (2-(-4))/(-5-5)= (6)/(-10)= -(3)/(5)`.

Thus, the slope n of the perpendicular line is
`\displaystyle{ (5)/(3)`.

The equation of the line with slope
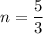
`\displaystyle{ n= (5)/(3)` containing the point M(0, -1) is given by:


`\displaystyle{ y-(-1)=(5)/(3)(x-0)`


`\displaystyle{ y+1= (5)/(3)x`


`\displaystyle{ 3y+3=5x`


`\displaystyle{ 5x-3y-3=0`

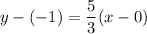
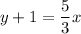
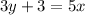
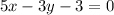
Answer: 5x-3y-3=0