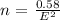From the question;
The number of voters randomly polled n is inversely proportional to the square of the desired margin of error E
This implies
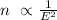
that is
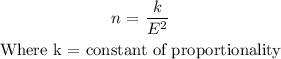
we are given
when, E = 0.1 (10%), n = 58 voters
we get
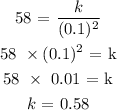
Therefore the connection between n and E is