So, we want to determine whether the lines:
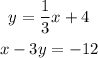
First, remember that there are two different ways to represent a line with an equation. These are:

Where m is the slope.
For example:

Where the slope is 1/3.
The second way, has the equation of the form:
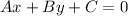
Where the slope is given by the operation:

For example:

Where the slope is:
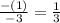
As you can see, both lines has the same slope, so, they are parallel.
Remember!
- Two lines are parallel if they have the same slope.
- Two lines are perpendicular if the product of their slopes is -1.