Question

Can you please help me solve this problem. I got A but am unsure.

Answer 1

Given these two series:

`\begin{gathered} \sum ^(\infty)_(n\mathop=1)(1)/(n^(2p)) \\ \sum ^(\infty)_{n\mathop{=}1}((p)/(2))^n \end{gathered}`

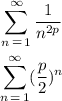
The second one is a way to write the geometric series, where r = p/2:

`\text{Geometric series}\colon\sum ^(\infty)_(n\mathop=1)r^n`

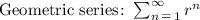
This series converges only if 0 < r < 1, so the condition of convergence of the second series is:

`\begin{gathered} 0\leq(p)/(2)<1 \\ 0\le p<2\ldots(1) \end{gathered}`

Now, for the first one, we know that the series diverges when 2p = 1, leading to the so-called Harmonic Series:

`\sum ^(\infty)_(n\mathop=1)(1)/(n)=\infty`

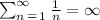
So, the condition of convergence should be:

`\begin{gathered} 2p>1 \\ p>(1)/(2)\ldots(2) \end{gathered}`

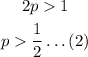
Combining these two conditions, (1) and (2), leads to:

[tex]\frac{1}{2}