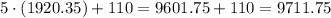Question

Sherrie invested some money at 13 % interest. Sherrie also invested $110 more than 5 times that amount at 8 % . How much is invested at each rate if Sherrie receives $1051.84 in interest after one year? (Round to two decimal places if necessary.)

Answer 1

We have two investments for Sherrie.

The first, an unknown amount X at 13% interest.

The second investment is a capital of $110 more than five times the amount X, invested 5 times within the year, at a rate of 8%.

The interest of the first investment, after one year (t=1), can be calcualted as:

`I_1=r_1X=0.13X`

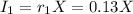
The interest for the second investment can be calculated as:

`\begin{gathered} FV=PV(1+(r_2)/(5))^5 \\ I_2=FV-PV=PV\lbrack(1+\frac{r^{}_2}{5})^5-1\rbrack \\ I_2=(110+5X)\lbrack(1+(0.08)/(5))^5-1\rbrack=(110+5X)\cdot(1\text{.}016^5-1) \\ I_2=(110+5X)\cdot(1.0826-1)=(110+5X)\cdot0.0826=9.09+0.413X \end{gathered}`

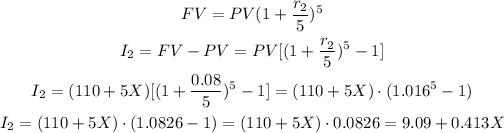
We know that the total interest in the year is $1051.84.

Then, the value X can be calculated as:

`\begin{gathered} I_1+I_2=0.13X+(9.09+0.413X)=1051.84 \\ 0.13X+0.413X=1051.84-9.09=1042.75 \\ X=(1042.75)/(0.543)=1920\text{.}35 \end{gathered}`

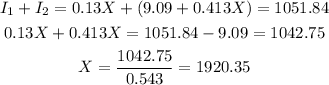
At 13% rate, Sherrie invested $1920.35.

At 8% rate, Sherrie invested $9711.75.

`5\cdot(1920.35)+110=9601.75+110=9711\text{.}75`