Question

Find out the number of combinations and the number of permutations for 8 objects taken 6 at a time. Express your answer in exact simplest form.

Answer 1

The permutation formula is expressed as

`\begin{gathered} P^n_r=(n!)/((n-r)!) \\ \end{gathered}`

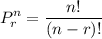
The combination formula is expressed as

`\begin{gathered} C^n_r=(n!)/((n-r)!r!) \\ \\ \end{gathered}`

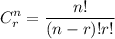
where

`\begin{gathered} n\Rightarrow total\text{ number of objects} \\ r\Rightarrow number\text{ of object selected} \end{gathered}`

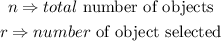
Given that 6 objects are taken at a time from 8, this implies that

`\begin{gathered} n=8 \\ r=6 \end{gathered}`

Thus,

Number of permuations:

`\begin{gathered} P^8_6=(8!)/((8-6)!) \\ =(8!)/(2!)=(8*7*6*5*4*3*2!)/(2!) \\ 2!\text{ cancel out, thus we have} \\ \begin{equation*} 8*7*6*5*4*3 \end{equation*} \\ \Rightarrow P_6^8=20160 \end{gathered}`

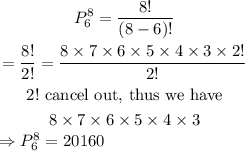
Number of combinations:

`\begin{gathered} C^8_6=(8!)/((8-6)!6!) \\ =(8!)/(2!*6!)=(8*7*6!)/(6!*2*1) \\ 6!\text{ cancel out, thus we have} \\ (8*7)/(2) \\ \Rightarrow C_6^8=28 \end{gathered}`

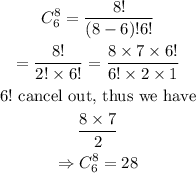
Hence, there are 28 combinations and 20160 permutations.