Answer:
2,700 years
Step-by-step explanation:
We were given the following details:
Half-life of carbon-14, T = 5600 years
78% of carbon-14 is left. This indicates that the amount of carbon-14 left is 78% of the initial amount:
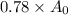
We will calculate the time since when the tree died as shown below:

Therefore, the tree died 2,700 years ago