Question

In a raffle where 8000 tickets are sold for $2 each, one prize of $4500 will be awarded. What is the expected value of a single ticket in the raffle?

Answer 1

Answer: -1.4375

The formula for the expected value goes by:

`E(x)=x_1P_1+x_2P_2`

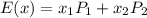
From the problem, we have 8000 tickets, and one will win a prize of $4500. This means that 7999 people will pay $2, with a probability of 7999/8000 losing, and the winner will get a value of $4500 - $2 = $4498, with a chance of 1/8000.

We now have:

x1 = -2

x2 = 4498

P1 = 7999/8000

P2 = 1/8000

Substituting to the equation and we will have:

`E(x)=x_1P_1+x_2P_2`
`E(x)=(-2)((7999)/(8000))+(4498)((1)/(8000))`
`E(x)=-1.4375`

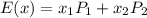
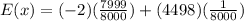
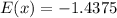
Therefore, the expected value of a single ticket is -1.4375.