Question

f(x)=4x^2-7x-15What are the x-intercepts of the graph of f(x)? Is the vertex going to be max or min? what are the coordinates of the vertex? what steps would I use to graph f(x)?

Answer 1

We are given the function

`f(x)=4x^2-7x-15`

To find the x - intercept, we will put f(x) = 0

`\begin{gathered} 4x^2-7x-15=0 \\ \\ using\text{ formula method} \\ \\ a=4 \\ b=-7 \\ c=-15 \\ \\ x=(-b\pm√(b^2-4ac))/(2a) \\ \\ x=(7\pm√(49-4(4)(-15)))/(2(4)) \\ \\ x=(7\pm√(289))/(8) \\ \\ x=(7\pm17)/(8) \\ \\ x=(24)/(8),(-10)/(8) \\ \\ x=3,-(5)/(4) \end{gathered}`

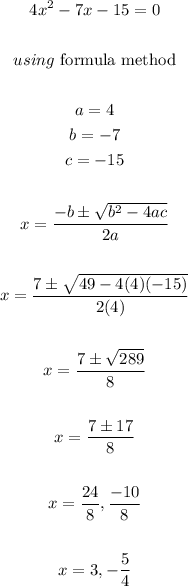
The x - intercept are

`\begin{gathered} x=3 \\ and \\ x=-(5)/(4) \end{gathered}`

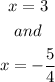
f(x) vertex is a minimum

`\begin{gathered} f(x)=4x^(2)-7x-15 \\ \\ f(x)=4(x^2-(7)/(4)x)-15 \\ \\ f(x)=4(x-(7)/(8))^2-4((7)/(8))^2-15 \\ \\ f(x)=4(x-(7)/(8))^2-4((49)/(64))-15 \\ \\ f(x)=4(x-(7)/(8))^2-(289)/(16) \end{gathered}`

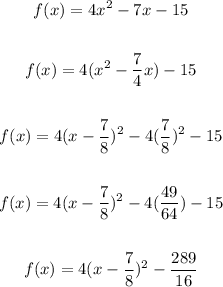
The coordinate of the vertex is

`((7)/(8),-(289)/(16))`

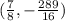
The graph of the function is

Basically, we use the vertex point, intercept on the x - axis and y - axis