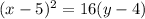Question

The equation of vertex: (5,4) focus: (5,8)

Answer 1

the equation of vertex: (5,4) focus: (5,8)​.

Since the x coordinates of vertex and focus are same, the focus and the vertex lies on the same vertical line, x=5. So, the parabla has vertical symmetry. The focus is above vertex as seen from the coordinates. So, the parabola opens upwards.

a=8-4=4.

The equation for vertical parabola is,

`\begin{gathered} (x-h)^2=4a(y-k) \\ \text{Here, (h,k ) is vertex.} \\ (h,k)=(5,4) \end{gathered}`

So, the equation of parabola can be obtained as,

`\begin{gathered} (x-5)^2=4*4(y-4) \\ (x-5)^2=16(y-4) \end{gathered}`

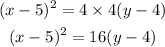
Therefore, the equation of parabola is

`(x-5)^2=16(y-4)`