Question

A crew of ten workers was hired to complete a job in 8 days. After working for two days, there was a new request to complete this job in two days. How many more workers need to be hired to finish this job in 2 days?

Answer 1

They would need to hire 20 more workers because they are 1/4 of the way done after the first two days. And that means they need to be 3/4 of the way done in the next 2 days, that means they have to be 3 times as productive from the first day and 10 times 3 equals 30, but they already have 10, so 30 - 10 = 20
THEY NEED 20 more workers
I hope it helps

Answer 2

29 more workers are needed.

Explanation:

Let us assume that the 10 workers, working at their normal rate would finish the job in exactly 8 days.

The rate of working for 1 worker is:

[ 1/10 of the job ] / [ 8 days ] = [ 1 job ] / [ 80 days ]

This is also [ 1/80 of the job ] / [ 1 day ]

In 2 days, the fraction of the job that gets done is:

`2* (1)/(80)=(1)/(40)`

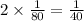
Job left =
`1-(1)/(40) =(39)/(40)`

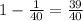
Now the rate has to be :

`((39)/(40) )/(2) =(39)/(80)`

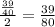
Now, let w be the additional number of workers needed.

We get:

`(10+w)/(80)=(39)/(80)`

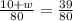
Solving for w;

`10+w=39`

`w=39-10`

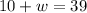
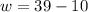
w = 29

Therefore, 29 more workers are needed.

-------------------------------------------------------------------------------------

There can be another approach as well.

Fraction of the job done by 10 workers in 2 days = 1/4

Remaining fraction = 1-1/4 = 3/4

Lets say W workers are needed more.

So, we can say that 3/4 of the work is to be done by 10+W workers.

Hence, it will take a total of 30 workers to complete the job.

Making it additional 20 workers.