Answer:
The time between hitting the ball and meeting the ground is
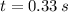
Step-by-step explanation:
We have a semi parabolic motion here. We know that the initial speed 216 km/h or 60 m/s in the x-direction.
So we can use the following equation:
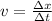


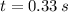
hope it helps you!