Answer:
The average velocity over the given interval = 4.13 m/s
Step-by-step explanation:
The initial velocity, v₀ = 350 m/s [55 degrees W of N]
The final velocity, vf = 150 m/s [30 degrees S of E]
Resolve the initial velcity to the x direction
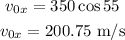
Resolve the initial velocity to the y direction
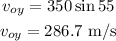
Resolve the final velocity to the x-direction
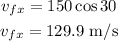
Resolve the final velocity to the y-direction
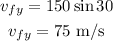
The acceleration in the x-direction
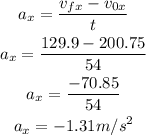
The acceleration in the y-direction
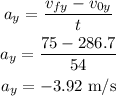
Find the resultant acceleration
![\begin{gathered} a=\sqrt[]{a^2_x+a^2_y} \\ a=\sqrt[]{(-1.31)^2+(-3.92)^2} \\ a=\sqrt[]{17.0825} \\ a=4.13\text{ m/s} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/physics/college/khfq6f9jgbmbijlrxdau.png)
The average velocity over the given interval = 4.13 m/s