Question

The Alisal school fall play was in October 2019. On the first day the school sold 15 student tickets and 10 adult tickets. They made $145. On the second day they made $203 and sold 21 student tickets and 14 adult tickets. How much was an adult ticket? How much was a student ticket?

Answer 1

Let x be the price of the student tickets and y the price of adult tickets.

We know that the first day there sold 15 students and 10 adults tickets and they earned 145, then:

`15x+10y=145`

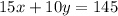
now, the second day they sold 21 student and 14 adult tickets and earned 203, then:

`21x+14y=203`

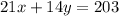
Then we hace the system:

`\begin{gathered} 15x+10y=145 \\ 21x+14y=203 \end{gathered}`

To solve this system we mutiply the second equation by -10 and the first by 14, then we have:

`\begin{gathered} 210x+140y=2030 \\ -210x-140y=-2030 \end{gathered}`

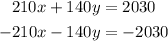
If we add this equations we have:

`0=0`

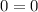
This means that we can not know the price of the tickets with the information given, since the information represent the same equation, and therefore the system of equations have an infinite number of solutions given by:

`y=(145)/(10)-(15)/(10)x`