Question

Write an algebraic equation of your choice must have the distributive property: __________________. Using the two-column proof below, solve your problem justifying each step. Listed are the properties used in algebraic proof. You may not use all of these.addition property of equalitysubtraction property of equalitydivision property of equalitymultiplication property of equalitySimplifyingdistributive property

Answer 1

We are tasked to write an algebraic equation with distributive property and solve it using the two-column proof.

For an algebraic equation, I will use the equation

`-3(x+1)+6x=15`

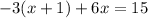
Let's start solving this problem by applying the distributive property on the first term -3(x+1). We have

`\begin{gathered} -3(x+1)=-3\cdot x+(-3)(1)=-3x-3 \\ \rightarrow\rightarrow-3x-3+6x=15 \end{gathered}`

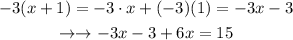
The next step is to add like terms. We add -3x and 6x on the left-hand side of the equation. We get

`\begin{gathered} -3x-3+6x=15 \\ \rightarrow3x-3=15 \end{gathered}`

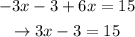
This will be followed by the addition property of equality. We add +3 on both sides of the equation so the -3 on the left-hand side of the equation will cancel out. We have

`\begin{gathered} 3x-3+3=15+3 \\ 3x=18 \end{gathered}`

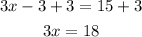
Finally, to solve the equation, we use the division property of equality. We divide both sides by 3. We get

`\begin{gathered} (3x)/(3)=(18)/(3) \\ x=6 \end{gathered}`

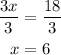
The steps are summarized as follows