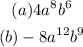Simplify the expression;

We shall apply the rule of exponent which is;
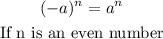
We now have;
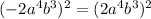
Next we shall apply the rule which is;
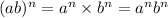
We now have the expression as;
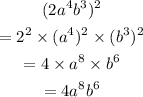
For the (b) part;

We shall apply the exponent rule;
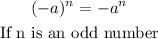
Our expression now becomes;
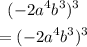
We shall also apply the second rule as stated earlier and we'll have;
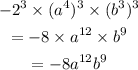
Step-by-step explanation:
An even exponent makes a negative number even as we have seen from our calculations. This is because the product of two negative numbers is positive, whereas an odd exponent makes a negative number odd because the product of three negative numbers like we saw in our calculation would be negative.
ANSWER: