Given: 10 district object to choose 6 objects
To Determine: The number of ways this can be done with and without attentionn to the order
(a) When the order of the choices does not matter, we will use combination principle. The formula for the number of combinations of r items from n choices is
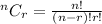
So the combination of 6 objects from 10 objects would be
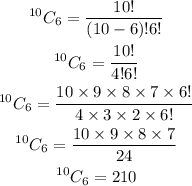
(b) When the order of the choices matter, we will use permutation principle. The formula for the number of permuating of r items from n choices is
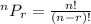
Therefore
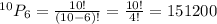
Hence,
(a) The number of ways if the order of the choices does not matter is 210 ways
(b) The number of ways if the order of the choices matter is 151200