Answer:
The energy stored in the spring when the bike goes over a bump is
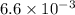 joules.
joules.
Step-by-step explanation:
Let suppose that spring has a linear behavious, by means of Hooke's Law, definition of Work and Work-Energy Theorem we find that the potential energy stored in the spring (
 ), measured in joules, is defined by:
), measured in joules, is defined by:
 (1)
(1)
Where:
 - Spring constant, measured in newtons per meter.
- Spring constant, measured in newtons per meter.
 - Deformation, measured in meters.
- Deformation, measured in meters.
If we know that
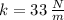 and
and
 , the energy stored by the spring due to compression is:
, the energy stored by the spring due to compression is:
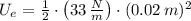
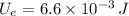
The energy stored in the spring when the bike goes over a bump is
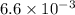 joules.
joules.