Question

Calc find the maximum of f(x, y) = y2 + xy â x2 on the square 0 ⤠x ⤠6, 0 ⤠y ⤠6.

Answer 1

Presumably,
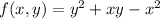
`f(x,y)=y^2+xy-x^2`. We have


`\begin{cases}f_x=y-2x=0\\f_y=2y+x=0\end{cases}`

`y=2x\implies 2y+x=4x+x=0\implies x=0\implies y=0`

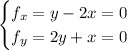
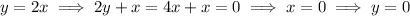
so on this region,
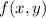
`f(x,y)` has only one critical point at (0, 0)[/tex]. Since this point lies on the boundary, we can ignore it for the moment.

Along the boundaries, we have four scenarios to consider:


`x=0\implies f(0,y)=y^2`

`x=6\implies f(6,y)=y^2+6y-36=(y+3)^2-45`

`y=0\implies f(x,0)=-x^2`

`y=6\implies f(x,6)=36+6x-x^2=-(x^2-6x-36)=45-(x-3)^2`

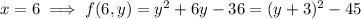
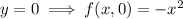
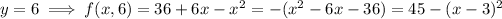
In the first case,
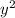
`y^2` is increasing over
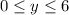
`0\le y\le6`, so we'll attain when
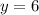
`y=6` a value of
`f(0,6)=36`.

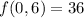
In the second case,
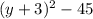
`(y+3)^2-45` attains a minimum when
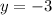
`y=-3`, and would be increasing to either side. This would mean at
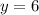
`y=6` we get
`f(6,6)=36`.

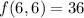
In the third case,
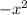
`-x^2` attains a max at
`x=0`, which would yield
`f(0,0)=0`.

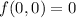
In the fourth case,
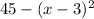
`45-(x-3)^2` attains a max at
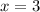
`x=3`, giving a value of
`f(3,6)=45`.

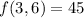
This means the absolute maximum of
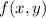
`f(x,y)` over the square is attained along the boundary
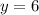
`y=6` when
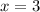
`x=3`, with a maximum value of
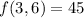
`f(3,6)=45`.