Question

Find the expected value for a fair six-sided dice roll.A. 2B. 2.5C. 3D. 3.5E. 4

Answer 1

D. 3.5

Step-by-step explanation:

A fair six-sided dice has faces labeled 1,2,3,4,5 and 6.

The probability of each of the faces occurring = 1/6

Thus, the expected value for a fair six-sided dice roll is:

`\begin{gathered} E(X)=\mleft(1*(1)/(6)\mright)+\mleft(2*(1)/(6)\mright)+\mleft(3*(1)/(6)\mright)+\mleft(4*(1)/(6)\mright)+\mleft(5*(1)/(6)\mright)+\mleft(6*(1)/(6)\mright) \\ =(1)/(6)+(2)/(6)+(3)/(6)+(4)/(6)+(5)/(6)+(6)/(6) \\ =(21)/(6) \\ =3.5 \end{gathered}`

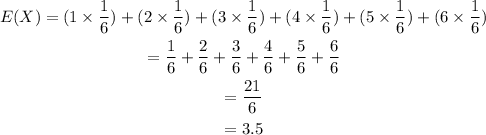
The expected value for a fair six-sided dice roll is 3.5.